Post You Might Like
Posted inGénérale Innovations Software
Laguira Maroc
Posted by
 By
admin
4 juillet 2025
By
admin
4 juillet 2025
Posted inGénérale Innovations Software
Panneau LEDs opticien
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025

Posted inGénérale
croissant leds pharmacie
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025
Posted inGénérale Innovations Software
Panneau LED dentiste
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025

Posted inGénérale Innovations Software
FAR: groupement B ratissage ZS
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025

Posted inGénérale Innovations Software
Justice etr justiciers
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025

Posted inGénérale Innovations Software
Ma plume et mes souffrances
Posted by
 By
admin
3 juillet 2025
By
admin
3 juillet 2025

Posted inGénérale Innovations Software
codage binaire hex.
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Mon banc d’essais par vidéos
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
Pharmacie de garde 7c
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Montage à 3 eprom
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
بصاريات اشهارية٢
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
Croissant LED pour pharmacie 7 sec.
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
Digitalisation : croix et croissants pharmacies.
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Enseignes publicitaires LED 3
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Maintien de l’ordre zone Sud Maroc
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Souvenirs militaires inoubliables SMI1
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
عبارة التهاني
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Flasher pour panneau totem
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Travaux: signalétique TS1
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
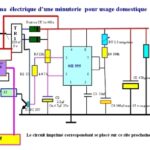
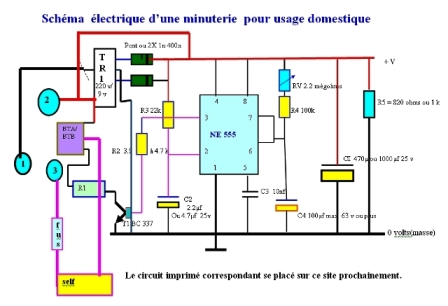
Éclairage escaliers LM 555
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Inverseur sextuple: OC 1
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Trois en un
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Mon banc d’essais: tech1
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Anniv. 14 mai 2025
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Circuits imprimés verre epoxy
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025

Posted inGénérale Innovations Software
Croissant LED
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025
Posted inGénérale Innovations Software
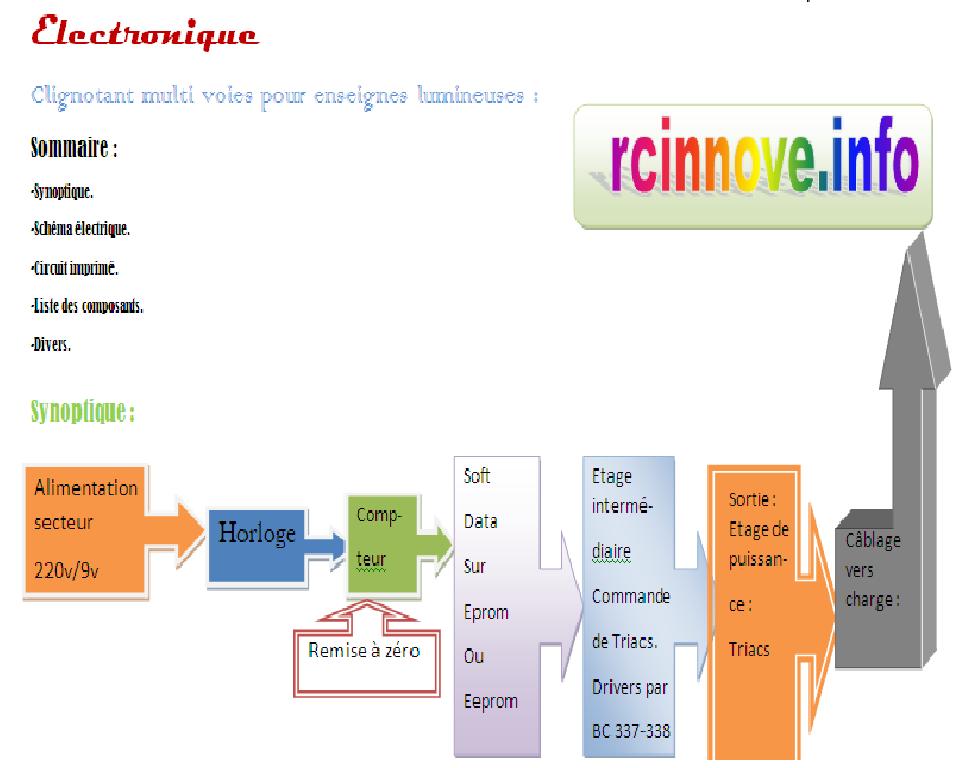
Editeur convertisseur simulateur 24 bits
Posted by
 By
admin
19 juin 2025
By
admin
19 juin 2025